La gravitation

I) Définitions

Une force est une grandeur vectorielle qui modélise une action qui peut :
– mettre un corps en mouvement ou au repos
– modifier le mouvement d’un corps
– déformer un objet
Elle se mesure en newton (N)

La position d'un corps représente l'emplacement de ce corps par rapport à un système de référence, le référentiel.
La vitesse est une grandeur qui mesure, pour un mouvement, le rapport de la distance parcourue au temps écoulé.
La vitesse instantanée est définie à un instant précis comme la dérivée de la position par rapport au temps $\frac{\mathrm{dx}}{\mathrm{dt}}$.
L’accélération est la variation de vitesse par unité de temps $\frac{\mathrm{dv}}{\mathrm{dt}}$ ou $\frac{\mathrm{d²x}}{\mathrm{dt²}}$

II) La loi de gravitation universelle

A) Définition

L’interaction gravitationnelle est l’une des quatre forces de l’univers. Elle modélise l’attraction entre les masses.
Sous forme vectorielle cette force est donnée par :
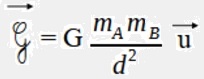avec :
-la force exercée de A sur B en newton (N)
- G la constante gravitationnelle universelle qui vaut 6,67 x 10 ^–11 N.kg ^².m ^–2
- m A la masse de A en kilogramme (kg)
- m B la masse de B en kilogramme (kg)
- d A-B la distance entre A et B en mètre (m)

L’intensité de cette force est :
F_A/B = G m_Am_B / d² Exemple G = 6,67 x 10 ^–11 N.kg ^².m ^–2 d Terre−Lune = 384 400 km
m Terre= 5,97 × 10 ²⁴ kg m Lune = 7,34 × 10 ²² kg Calculer la force gravitationnelle entre la Terre et la Lune.

B) Le poids

Le poids est la force de gravitation à la surface d’un astre. Par exemple si on reprend la formule en l’appliquant à la surface de la Terre :
F_A/B = G m_A m_B / d ² = G m_Terre m_B / r²_Terre

Dans cette formule la masse de la Terre, G et le rayon terrestre sont des constantes qui sont regroupés sous la constante g Terre D’où P = mg Avec g Terre qui vaut environ 9,81 N/kg.

Activité

Aristote vs Galilée vs Newton

Aristote

« Tout ce qui est en mouvement est nécessairement mû par quelque chose.
Si donc il n’a pas en lui-même le principe de son mouvement –comme les êtres vivants il est évidemment mû par un autre ». (Physique(VII, I)).
« Un corps en mouvement s’arrête quand la force qui le pousse ne peut plus agir de façon à le pousser. » (Mécaniques)

Galilée

« Le mouvement est mouvement et agit comme mouvement en tant seulement qu’il est en rapport avec les choses qui en sont privées ; mais en ce qui concerne celles qui y participent toutes également, il est sans effet »
(Dialogue, Galilée, Ed. nat. p.141, trad. Koyré) « J’imagine qu’un mobile a été lancé sur un plan horizontal d’où l’on a écarté tout obstacle ; il est déjà certain, d’après ce qu’on a dit ailleurs plus longuement, que son mouvement se poursuivra uniformément et éternellement sur ce même plan pourvu qu’on le prolonge à l’infini.». Traduction de Maurice Clavelin, p.205

Newton

Définition de la force imprimée : « La force imprimée (vis impressa) est une action exercée sur le corps, qui a pour effet de changer son état de repos ou de mouvement uniforme en ligne droite ».
Première loi de la mécanique: “Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme à moins que des forces imprimées ne le contraignent à changer son état” (Loi I, traduction de l’édition de 1727 par la marquise du Chastelet).
Corollaire V : « Les mouvements des corps inclus dans un espace donné sont les mêmes, entre eux, que cet espace soit au repos, ou qu’il se meuve uniformément en ligne droite sans mouvement circulaire »

Correction

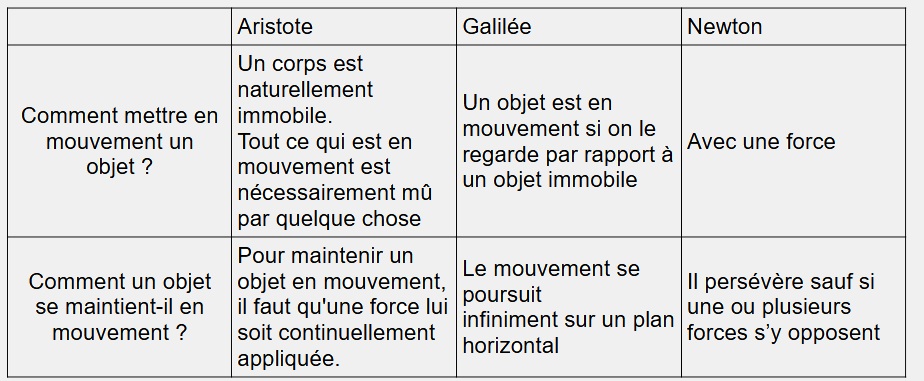
1) En réfléchissant à des mouvements d’objets simples, ou en vous appuyant sur les situations pensez-vous que la mise en mouvement d’un objet nécessite toujours une force ? 2) Pensez-vous que modifier un mouvement (uniforme, accéléré ou ralenti) nécessite une force ? 3) Après avoir lu les textes des 3 savants, remplissez ce tableau :

Activité

Différences temps de chute

Rappels

2 ^ème loi de Newton :
Σ $\overrightarrow{F}$ = m $\overrightarrow{a}$


Poids $\overrightarrow{P}$ = m $\overrightarrow{g}$
avec g = 10 m/s²

Hypothèse de la chute libre :
Un objet en chute n’est soumis qu’à son poids

I) Différence de masse

On dispose de deux objets l’un de masse de m₁ = 100 g et m₂ = 200 g.
On les lâche d’une hauteur de 10 m sans vitesse initiale.
Calculer le temps de chute des ses deux objets.

II) Différence de hauteurs

Calculer le temps de chute pour une hauteur de 20, 30 et 40 m.
Comparer ces résultats.

III) L’énergie

L’énergie est une grandeur physique qui mesure la capacité à modifier son environnement, elle se mesure en joule.
L’énergie existe sous 6 formes : nucléaire, thermique, mécanique, électrique, chimique et lumineuse.

IV) Énergie mécanique

L’énergie mécanique est définie par la somme de l’énergie cinétique et de l’énergie potentielle de pesanteur. Énergie cinétique : E_c = $\frac{1}{2}$ m v²
Énergie potentielle de pesanteur :
E _pp = m g z

Énergie mécanique :
E _m = E _c +E _pp

Si une force ne fait pas varier l’énergie mécanique elle est dite conservative.
Si toutes les forces appliquées à un système sont conservatives ou si la somme des travaux des forces non conservatives est nulle alors la variation d’énergie mécanique est nulle, soit :
Δ E _m = 0

V) Lois de Kepler

Au 17 ème siècle Kepler énonce trois lois décrivant les mouvements des planètes autour du Soleil.

Première loi
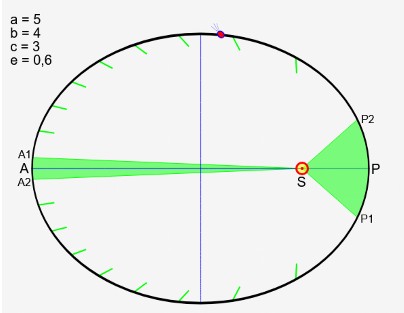
Les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l'un des foyers.

Deuxième loi
Des surfaces égales sont balayées dans des temps égaux.

Troisième loi

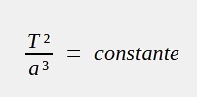
Pour un mouvement circulaire dans le système solaire :

Exercice 1

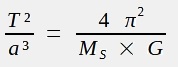
Europe est un satellite de Jupiter, de masse M _J.
Son orbite, de rayon r, est supposée circulaire.
Sa vitesse a pour valeur
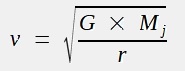
1) Établir l'expression de sa période de révolution T.
2) En déduire la valeur du rapport.
3) Énoncer la troisième loi de Kepler dans le référentiel « jupiterocentrique ».
Exercice 2 Le tableau ci-dessous donne la période de révolution de quelques planètes du système solaire, ainsi que le rayon de leur orbite assimilable à un cercle dans le référentiel héliocentrique.

Exercice 2

Le tableau ci-dessous donne la période de révolution de quelques planètes du système solaire, ainsi que le rayon de leur orbite assimilable à un cercle dans le référentiel héliocentrique.

1) Établir l'expression de la valeur de la vitesse du centre de masse d'une de ces planètes dans le référentiel héliocentrique.
2) En déduire l'expression de sa période de révolution en fonction de G, r et Ms (masse du Soleil).
3) Donner l'expression du rapport dans le référentiel héliocentrique.
La troisième loi de Kepler est-elle vérifiée ?
4) Déterminer la masse Ms du Soleil.

Données :
• Constante universelle de gravitation : G = 6,67 x 10 ^–11 N.kg ^².m ^–2
1 année = 3,156 x 10 ⁷ s.

Exercice 3

Un fruit, accroché à un arbre, tombe sur le sol. On néglige l'action de l'air sur le fruit au cours de la chute.
1) Dans un référentiel terrestre, exprimer l'énergie mécanique du fruit:
a) lorsqu'il est encore accroché dans l'arbre;
b) juste avant qu'il ne touche le sol.
2) Indiquer pourquoi on peut considérer que cette énergie est constante lors du mouvement du fruit.